Fortran
2021-01-19
1 Basics
1.1 Module
1.1.1 Explanation on submodule
Submodules are a feature added to the language to address one specific question: separation of interface and implementation. The main motivation was the compile cascades generated when you needed to change just a implementation detail in a module.
But Submodules are not Modules!
A submodule is tied to a module and provides implementation to procedures declared in that module. So, a submodule have access to all declarations in it’s parent module. Nonetheless, the module doesn’t know anything about it’s Submodules, and doesn’t USE it’s Submodules like they were modules. The module just expect you to add Submodules at link time, enough to cover all the missing procedure implementations.
Reference: Puting derived types with procedures from module to submodule
1.2 I/O
The direct attribute of the open procedure
does not add header and footer information to each record. Fortran’s
default behavior is the sequential access with header and
footer included. The header and footer store the size of each record. It
seems like both of them store the same info, i.e. the size of bytes of
each record. Check Best
answer to: Opening Binary Files in Fortran: Status, Form, Access for
reference.
1.2.1 Binary/Hex Representation of Number
Negative integer represented in binary form uses the two component
system. Basically it is \(2^m - n\)
where \(-n\) is the negative number and
\(m\) is the number of digits in the
binary format. For example, \(2^8 - 10 =
246\). 10 is 0a. -10 is
f6.
To check the content of a bindary file, in Linux, use
hexdump or xxd. I prefer xxd.
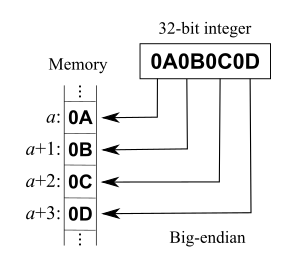
1.2.2 Big Endian and Little Endian
For the illustration of the big endian and little endian, check the Wikipedia link. It seems like Linux use little endian as the default option.

1.2.3 Example
program io
implicit none
continue
call writeBinFile()
contains
subroutine writeBinFile()
integer(4) :: i = 10
continue
open(unit=1, file='data_direct_access.bin', form='unformatted', &
access='direct', recl=1, status='unknown')
write(unit=1, rec=1) i
write(unit=1, rec=2) i*2
close(unit=1)
!
open(unit=2, file='data_sequential_access.bin', form='unformatted', &
access='sequential', status='unknown')
write(unit=2) i
write(unit=2) i*2
close(unit=2)
end subroutine writeBinFile
end programThe output is as follows,
-rw-rw-r--. 1 jcshi jcshi 8 Mar 1 18:08 data_direct_access.bin
-rw-rw-r--. 1 jcshi jcshi 24 Mar 1 18:08 data_sequential_access.bin
xxd data_sequential_access.bin
00000000: 0400 0000 0a00 0000 0400 0000 0400 0000 ................
00000010: 1400 0000 0400 0000 ........
xxd data_direct_access.bin
00000000: 0a00 0000 1400 0000 ........2 integers of 4 bytes are 8 bytes. It is using the little endian.
0a00 0000 is 10, 1400 0000 is
20. The header and footer store the size of bytes
4.
1.2.4 Use Python to Manipulate Fortran Binary File
scipy.io.FortranFile
could be used to read in Fortran binary file to check it content.
1.3 Array
1.3.1 Equivalent to MATLAB
find
I = pack([(j,j=1,size(v))],v==3)1.3.2 Avoid Temporary Array Created
When the actual argument array (i.e. declared in the calling routine) is deferred-shape or assumed-shape array and the dummy argument array (i.e. declared in the routine being called) is the explicit-shape array, the program will create an temporary array which slows the program a lot. Check this link for the details.
The array temporary is created because the passed array may not be contiguous and the receiving (explicit-shape) array requires a contiguous array. When an array temporary is created, the size of the passed array determines whether the impact on slowing run-time performance is slight or severe.
The following codes illustrate it. The function
func_explicit_shape declares an explicit-shape array
in_arr(1:n1,1:n2) while func_deferred_shape
uses a deferred-shape array in_arr(:,:) where the shape of
the array is obtained by the intrinsic function size().
program test
!
integer :: n1,n2, i,nt
real(4), dimension(:,:), allocatable :: arr1
real(4), dimension(:), allocatable :: arr2
real(4) :: tb,te
!
continue
!
n1 = 4
n2 = 10240
allocate(arr1(1:n1,1:n2))
allocate(arr2(1:n2))
!
arr1 = 4
n1 = 2
n2 = 5120
nt = 200000
!
call cpu_time(tb)
do i = 1, nt
arr2(n2:n2*2-1) = func_explicit_shape(arr1(n1:n1+1,n2:n2*2-1),2,n2)
arr1(n1,n2:n2*2-1) = arr2(n2:n2*2-1)
end do
call cpu_time(te)
write(*,11) te-tb
call cpu_time(tb)
do i = 1, nt
arr2(n2:n2*2-1) = func_deferred_shape(arr1(n1:n1+1,n2:n2*2-1))
arr1(n1,n2:n2*2-1) = arr2(n2:n2*2-1)
end do
call cpu_time(te)
write(*,12) te-tb
deallocate(arr1)
deallocate(arr2)
!
11 format("explicit shaped array costs ",f10.2," seconds")
12 format("deferred shaped array costs ",f10.2," seconds")
!
contains
!
pure function func_explicit_shape(in_arr,n1,n2) result(return_value)
!
real(4), intent(in) :: in_arr(1:n1,1:n2)
integer, intent(in) :: n1,n2
real(4) :: return_value(1:n2)
!
integer :: i
!
continue
!
do i = 1,n2
return_value(i) = sum( in_arr(1:n1,i) )
end do
!
end function func_explicit_shape
!
pure function func_deferred_shape(in_arr) result(return_value)
!
real(4), intent(in) :: in_arr(:,:)
real(4) :: return_value(1:size(in_arr,dim=2))
!
integer :: n1,n2
integer :: i
!
continue
!
n1 = size(in_arr,dim=1)
n2 = size(in_arr,dim=2)
do i = 1,n2
return_value(i) = sum( in_arr(1:n1,i) )
end do
!
end function func_deferred_shape
!
end programUsing the Intel Fortran compiler ifort with
-O3 -xHost enabled, the performance of the two versions are
compared as follows,
# jcshi @ master in ~/learn [21:26:10]
$ ./test_opt
explicit shaped array costs 1.53 seconds
deferred shaped array costs 1.00 seconds
# jcshi @ master in ~/learn [21:26:17]
$ ./test_opt
explicit shaped array costs 1.64 seconds
deferred shaped array costs 1.00 seconds
# jcshi @ master in ~/learn [21:26:22]
$ ./test_opt
explicit shaped array costs 1.54 seconds
deferred shaped array costs 1.00 secondsThe Intel Fortran compiler has a flag
-check arg_temp_created to check if an temporary array is
created. With this flag, run the debug version will give the following
warning,
forrtl: warning (406): fort: (1): In call to FUNC_EXPLICIT_SHAPE, an array temporary was created for argument #11.3.3 Set Multidimensional Array
integer :: cell_face_cnt_dir(1:2,1:6,1:3) = 0
cell_face_cnt_dir(1:2,1:6,3) = reshape( &
[ 1, 1, 2, 1, 2, 1, &
2, 3, 3, 3, 3, 2 ], shape = [ 2, 6 ], order = [ 2, 1 ] )2 Advanced
2.1 OOP
2.1.1 FINAL: finalizer
of class
One example is as follows. No memory will be lost. Note that the defined type will be reclaimed after leaving a subroutine.
def.f90 is as follows,
module def_mod
!
implicit none
!
public
!
type :: time_info_t
!
integer :: it = -1
real :: time = -1.0
real, dimension(:), allocatable :: arr
!
contains
!
procedure :: Init => InitTimeInfo
! final :: Decontructor => DestroyTimeInfo ! invalid syntax
final :: DestroyTimeInfo
!
end type time_info_t
!
interface time_info_t
module procedure TimeInfoConstructor
end interface
!
contains
!
function TimeInfoConstructor() result(time_info)
!
type(time_info_t) :: time_info
!
continue
!
time_info%it = 5
time_info%time = 5.0
allocate(time_info%arr(1:5),source=5.0)
write(*,*) "TimeInfoConstructor"
!
end function TimeInfoConstructor
!
subroutine InitTimeInfo(this)
!
class(time_info_t) :: this
!
continue
!
this%it = 0
this%time = 0.0
allocate(this%arr(1:5),source=0.0)
write(*,*) "InitTimeInfo"
!
end subroutine InitTimeInfo
!
subroutine DestroyTimeInfo(this)
!
type(time_info_t) :: this
!
continue
!
if (allocated(this%arr)) then
deallocate(this%arr)
end if
write(*,*) "DestroyTimeInfo"
!
end subroutine DestroyTimeInfo
!
end module def_modmain.f90 is as follows,
program main
!
use def_mod, only : time_info_t
!
implicit none
!
type(time_info_t), allocatable :: tinfo
!
continue
! No mem lost after calling test().
call test()
! Also no mem lost.
allocate(tinfo, source=time_info_t())
write(*,*) tinfo%it, tinfo%time
deallocate(tinfo)
!
contains
!
subroutine test()
!
type(time_info_t) :: tinfo
!
continue
!
call tinfo%Init()
write(*,*) tinfo%it, tinfo%time
!
end subroutine test
!
end program main2.1.2 Function as user-defined type constructor
module Defs
implicit none
private
public point, point2d, container
type, abstract :: point ! Abstract parent type
contains
procedure(func), deferred :: radius ! Prototype for func supplied by abstract interface
end type point
abstract interface
real function func( this )
import point ! Need to import type information into interface
class(point) this
end function func
end interface
type, extends(point) :: point2d ! Child type
real x, y
contains
procedure :: radius => r2d
end type point2d
type :: container
class(point), allocatable :: ptr
end type container
interface point2d
module procedure :: myinit
end interface
contains
!-----------------------------------
real function r2d( this )
class(point2d) this
r2d = sqrt( this%x ** 2 + this%y ** 2 )
end function r2d
!-----------------------------------
type(point2d) function myinit()
myinit%x = 10
myinit%y = 10
end function myinit
end module Defs
!===========================================================
program main
use Defs
implicit none
type(container), allocatable :: arr(:)
type(point2d) :: b
allocate(container::arr(2))
arr(1)%ptr=point2d( 3, 4 )
write(*, *) "2-d radius is ", arr(1)%ptr%radius()
b = point2d()
write(*, *) b%x, b%y, b%radius()
end program main2.1.3 Polymorphic variable
The polymorphic variable should be a feature of the Fortran 2003. But Fortran 2018 should be better. Intel compiler 17 does not support it. I use Intel compiler 19 with update 1 to compile the following codes.
module Defs
implicit none
private
public point, point2d, point3d, container
type, abstract :: point ! Abstract parent type
contains
procedure(func), deferred :: radius ! Prototype for func supplied by abstract interface
end type point
abstract interface
real function func( this )
import point ! Need to import type information into interface
class(point) this
end function func
end interface
type, extends(point) :: point2d ! Child type
real x, y
contains
procedure :: radius => r2d
end type point2d
type, extends(point2d) :: point3d ! Grandchild type!
real z
contains
procedure :: radius => r3d
end type point3d
type :: container
class(point), allocatable :: ptr
end type container
contains
!-----------------------------------
real function r2d( this )
class(point2d) this
r2d = sqrt( this%x ** 2 + this%y ** 2 )
end function r2d
!-----------------------------------
real function r3d( this )
class(point3d) this
r3d = sqrt( this%x ** 2 + this%y ** 2 + this%z ** 2 )
end function r3d
!-----------------------------------
end module Defs
!===========================================================
program main
use Defs
implicit none
type(container), allocatable :: arr(:)
allocate(container::arr(2))
arr(1)%ptr=point2d( 3, 4 )
write(*, *) "2-d radius is ", arr(1)%ptr%radius()
arr(2)%ptr=point3d( 3, 4, 5 )
write(*, *) "3-d radius is ", arr(2)%ptr%radius()
end program main2.2 Practices
2.2.1 Passing null pointer
Reference: Passing a null pointer actual argument to a member procedure of a derived type
2.2.2 Multidimensional Array
The performance of single dimensional array verus the
multidimensional array is shown as follows. The Fortran program is
compiled using the Intel compiler ifort 17.0.5 with the
optimization flag -O3 -xHost. 10 times running shows that
arr3(1:10240)%v(1:4,1:50,1:2) is faster than
arr3(1:10240)%v(1:1,1:400,1:1). However,
arr3(1:10240)%v(1:1,1:512,1:1) is faster than
arr3(1:10240)%v(1:4,1:64,1:2). I attribute this behavior to
the vectorization. The multidimensional array performs similarly to the
one dimensional array.
$ ~/software_profile/linux/time_sampling.sh /home/jcshi/learn/test_opt_1-512-1 10
No.1 run, the user time is 3.56s.
No.2 run, the user time is 3.48s.
No.3 run, the user time is 3.37s.
No.4 run, the user time is 3.35s.
No.5 run, the user time is 3.37s.
No.6 run, the user time is 3.47s.
No.7 run, the user time is 3.42s.
No.8 run, the user time is 4.48s.
No.9 run, the user time is 3.40s.
No.10 run, the user time is 3.41s.
Time sampling 10 times, with the averaged user time 3.5310s.
$ ~/software_profile/linux/time_sampling.sh /home/jcshi/learn/test_opt_4-64-2 10
No.1 run, the user time is 3.73s.
No.2 run, the user time is 3.69s.
No.3 run, the user time is 3.91s.
No.4 run, the user time is 3.85s.
No.5 run, the user time is 3.99s.
No.6 run, the user time is 3.72s.
No.7 run, the user time is 4.25s.
No.8 run, the user time is 4.15s.
No.9 run, the user time is 4.73s.
No.10 run, the user time is 3.58s.
Time sampling 10 times, with the averaged user time 3.9600s.The source codes are as follows,
program test
!
type :: dof_t
real(8), dimension(:,:,:), allocatable :: v
end type dof_t
!
integer :: n,i, n1,n2,n3, k
type(dof_t), dimension(:), allocatable :: arr3
real :: tb,te
!
continue
!
n = 10240
allocate(arr3(1:n))
!
call cpu_time(tb)
!
! n1 = 1
! n2 = 400
! n3 = 1
n1 = 4
n2 = 50
n3 = 2
do i = 1,n
allocate(arr3(i)%v(1:n1,1:n2,1:n3))
end do
!
do k = 1,1000
!
do i = 1,n
arr3(i)%v(1:n1,1:n2,1:n3) = 100
arr3(i)%v(1:n1,1:n2,1:n3) = arr3(i)%v(1:n1,1:n2,1:n3)**2
end do
!
end do
!
call cpu_time(te)
! write(*,*) te-tb
!
do i = 1,n
deallocate(arr3(i)%v)
end do
deallocate(arr3)
!
end program2.2.3 Array of Pointer
real, dimension(:), pointer :: ptr does not define an
array of pointers, but a pointer to an array.
One way of defining the array of pointer is to define a type of pointer and create an array of that type.
type domainptr
type(domain), pointer :: p
end type mytype
type(domainptr), dimension(3) :: dom
dom(1)%p => d01
dom(2)%p => d02
dom(3)%p => d03However, the pointer prevents the vectorization optimization. Check the following example code.
program test
integer, parameter :: wp = 8
type :: q_ptr
real(wp), dimension(:,:), pointer, contiguous :: p
end type q_ptr
type(q_ptr), dimension(1:2,1:2) :: q_ptr_mat
real(wp), dimension(:,:), allocatable, target :: a,b,c
real(wp) :: time_beg, time_end, s
integer :: nq, npts, i
continue
call cpu_time(time_beg)
nq = 4
npts = 256*1024*128
allocate(a(1:nq,1:npts))
allocate(b(1:nq,1:npts))
allocate(c(1:nq,1:npts))
call random_number(a)
call random_number(b)
call random_number(c)
call random_number(s)
q_ptr_mat(1,1)%p => a
q_ptr_mat(2,1)%p => b
q_ptr_mat(1,2)%p => c
! the pointer way
!DIR$ IVDEP
do i = 1, 50
q_ptr_mat(1,2)%p(:,:) = q_ptr_mat(2,1)%p(:,:) * s - q_ptr_mat(1,1)%p(:,:)
end do
! the direct way
! !DIR$ IVDEP
! do i = 1, 50
! c = b * s - a
! end do
call cpu_time(time_end)
write(*,"('Elapsed time: ',f6.3)") time_end - time_beg
end programUse the Intel Fortran compiler to compile the optimized version
ifort -O3 -xHost -qopt-report=5 -o test_opt test.f90. The
optimization report is saved to test.optrpt. The pointer
way produces a different report compared to that by the direct way. The
key is if the compiler is able to vectorize
q_ptr_mat(1,2)%p(:,:) = q_ptr_mat(2,1)%p(:,:) * s - q_ptr_mat(1,1)%p(:,:)
or c = b * s - a. The report file of the pointer way shows
as follows,
LOOP BEGIN at test.f90(25,3)
remark #25096: Loop Interchange not done due to: Imperfect Loop Nest (Either at Source or due to other Compiler Transformations)
remark #25452: Original Order found to be proper, but by a close margin
remark #15344: loop was not vectorized: vector dependence prevents vectorization
remark #15346: vector dependence: assumed OUTPUT dependence between Q_PTR(1,2,:,:) (26:5) and Q_PTR(1,2,:,:) (26:5)
remark #15346: vector dependence: assumed OUTPUT dependence between Q_PTR(1,2,:,:) (26:5) and Q_PTR(1,2,:,:) (26:5)
LOOP BEGIN at test.f90(26,5)
remark #15344: loop was not vectorized: vector dependence prevents vectorization
remark #15346: vector dependence: assumed FLOW dependence between Q_PTR(1,2,:,:) (26:5) and Q_PTR(2,1,:,:) (26:5)
remark #15346: vector dependence: assumed ANTI dependence between Q_PTR(2,1,:,:) (26:5) and Q_PTR(1,2,:,:) (26:5)
LOOP BEGIN at test.f90(26,5)
remark #15344: loop was not vectorized: vector dependence prevents vectorization
remark #15346: vector dependence: assumed FLOW dependence between Q_PTR(1,2,:,:) (26:5) and Q_PTR(2,1,:,:) (26:5)
remark #15346: vector dependence: assumed ANTI dependence between Q_PTR(2,1,:,:) (26:5) and Q_PTR(1,2,:,:) (26:5)
LOOP END
LOOP END
LOOP ENDIt shows that the compiler assumes that q_ptr has
dependence among its elements even though the compiler directive
!DIR$ IVDEP is added for that loop to tell the compiler
that this loop has no dependence. However, the direct way does not show
such dependence as follows,
LOOP BEGIN at test.f90(29,3)
remark #25096: Loop Interchange not done due to: Imperfect Loop Nest (Either at Source or due to other Compiler Transformations)
remark #25451: Advice: Loop Interchange, if possible, might help loopnest. Suggested Permutation : ( 1 2 3 ) --> ( 2 1 3 )
remark #15542: loop was not vectorized: inner loop was already vectorized
LOOP BEGIN at test.f90(30,5)
remark #15542: loop was not vectorized: inner loop was already vectorized
LOOP BEGIN at test.f90(30,5)
<Peeled loop for vectorization>
remark #25015: Estimate of max trip count of loop=3
LOOP END
LOOP BEGIN at test.f90(30,5)
remark #15388: vectorization support: reference C(:,:) has aligned access
remark #15389: vectorization support: reference B(:,:) has unaligned access
remark #15389: vectorization support: reference A(:,:) has unaligned access [ test.f90(30,11) ]
remark #15381: vectorization support: unaligned access used inside loop body
remark #15305: vectorization support: vector length 4
remark #15399: vectorization support: unroll factor set to 4
remark #15309: vectorization support: normalized vectorization overhead 0.472
remark #15300: LOOP WAS VECTORIZED
remark #15321: Compiler has chosen to target XMM/YMM vector. Try using -qopt-zmm-usage=high to override
remark #15442: entire loop may be executed in remainder
remark #15449: unmasked aligned unit stride stores: 1
remark #15450: unmasked unaligned unit stride loads: 2
remark #15475: --- begin vector cost summary ---
remark #15476: scalar cost: 8
remark #15477: vector cost: 2.250
remark #15478: estimated potential speedup: 3.150
remark #15488: --- end vector cost summary ---
LOOP END
LOOP BEGIN at test.f90(30,5)
<Remainder loop for vectorization>
remark #15389: vectorization support: reference C(:,:) has unaligned access
remark #15389: vectorization support: reference B(:,:) has unaligned access
remark #15389: vectorization support: reference A(:,:) has unaligned access [ test.f90(30,11) ]
remark #15381: vectorization support: unaligned access used inside loop body
remark #15305: vectorization support: vector length 4
remark #15309: vectorization support: normalized vectorization overhead 1.818
remark #15301: REMAINDER LOOP WAS VECTORIZED
LOOP END
LOOP BEGIN at test.f90(30,5)
<Remainder loop for vectorization>
LOOP END
LOOP END
LOOP END- For the pointer alising, refer to Vectorization: Pointer Aliasing.
- For the Intel compiler directive, refer to
2.2.4 Common Causes of Segmentation Faults (Segfaults)
Check Common Causes of Segmentation Faults (Segfaults). Or check this PDF.
However, the location of the segmentation fault might not be the root problem—a segfault is often a symptom, rather than the cause of a problem.